Вход или Регистрация

| СТАТЬИ
И ПУБЛИКАЦИИ
Вход или Регистрация |
ПОМОЩЬ В ПАТЕНТОВАНИИ | НАУЧНО-ТЕХНИЧЕСКИЙ ФОРУМ | Научно-техническая
библиотека |
ЧАСТОТНО-ИЗБИРАТЕЛЬНАЯ ФИЛЬТРАЦИЯ В ИНФОРМАЦИОННЫХ ТЕХНОЛОГИЯХ ОБРАБОТКИ СИГНАЛОВ
УДК 681.3.06.14
Опубликовано в журнале "Управляющие системы и машины", 2002, № 2, с.54-59.
© Леонид Соломонович Файнзильберг, к.т.н.
Контакт с автором: fainzilberg@svitonline.com
Рассмотрен подход к построению цифровых фильтров частотных помех, основанный на прямом и обратном дискретном преобразовании Фурье. Отличительной особенностью предложенного алгоритма является применение дополнительной процедуры “контрастирования” спектра гармонической помехи. Приведены результаты тестирования разработанного алгоритма на реальных и модельных примерах
Введение. Предварительная обработка данных является одной из актуальных задач, возникающих при построении информационных технологий обработки сигналов различной физической природы [1]. В первую очередь эта задача связана с выделением полезного сигнала на фоне помех: требуется по сигналу y[n] = f(x[n],e [n]), наблюдаемому в дискретные моменты времени n = 1,…, N, отделить полезный сигнал x[n] от искажающей его помехи e [n].
Понятно, что такая задача имеет решение только в том случае, когда априори известна либо сделаны обоснованные допущения о функции f(.). Довольно часто предполагается, что помеха аддитивна, т.е. y[n] = x[n] + e [n] [2]. Но даже при таких предположениях возможно отделить полезный сигнал от помехи, если имеются различия в их характеристиках (частотных, вероятностных и т.п.).
В тех случаях, когда модель полезного сигнала x[n] может быть описана с точностью до небольшого числа параметров, решение задачи сводится к оценке этих параметров по наблюдаемой реализации. Такой подход возможен при обработке зашумленных сигналов, порождаемых в процессе функционирования достаточно простых технических систем.
В то же время часто модель полезного сигнала либо неизвестна, либо достаточно сложна, чтобы можно было свести задачу отделения полезного сигнала от помехи к оценке небольшого числа параметров. Такая ситуация характерна при обработке электрокардиограмм [3], магнитокардиограмм [4], термограмм кристаллизации металла [5] и других сигналов сложной структуры, порожденных живой природой, а не технической системой.
В таких ситуациях не остается ничего иного, как ввести адекватные предположения о модели помехи и строить различные фильтры, обеспечивающие максимально возможное удаление помехи при минимальных искажениях полезного сигнала.
В настоящей статье развивается и исследуется один из возможных подходов к решению задачи фильтрации частотных помех, основанный на прямом и обратном дискретном преобразовании Фурье (ДПФ).
Постановка задачи.
Пусть на вход системы предварительной
обработки данных поступает сигнал
y[n], который измерен в
дискретные моменты времени
n = 1,2,…,N
и содержит информацию о полезном сигнале x[n],
зашумленном аддитивной помехой e
[n]
y [n] = x [n] + e [n]. (1)
Будем полагать, что помеха e имеет частотную природу и может быть представлена суммой стационарных гармонических колебаний
e [n]
= ![]() ai
sin (2 πfi n
+j i)
(2)
ai
sin (2 πfi n
+j i)
(2)
с априори известными
частотами fi и
неизвестными амплитудами ai
и
фазами j i.
Традиционно для цифровой фильтрации таких сигналов используют различные фильтры с бесконечной или конечной импульсной характеристикой, в частности, широко известный фильтр Баттерворта [6,7]. Основным их преимуществом является возможность обработки сигнала в реальном масштабе времени по мере поступления очередного дискретного отсчета y [n].
В то же время всем таким фильтрам присущи следующие недостатки. Во-первых, они позволяют устойчиво фильтровать сигнал лишь после определенного промежутка времени, зависящего от параметров настройки фильтра, в частности, от его порядка. Во-вторых, даже при оптимальной настройке таких фильтров не удается реализовать “идеальную” амплитудно-частотную характеристику (АЧХ), обеспечивающую полное подавление частот в полосе заграждения без искажения сигнала в полосе пропускания. Реально эти фильтры позволяют лишь аппроксимировать “идеальную” АЧХ прямоугольной формы с некоторой степенью точности. Особые трудности синтеза таких фильтров вызывают практически важные случаи, когда требуется обеспечить узкополосную режекцию сигнала (меньше 0.1% частоты дискретизации).
Именно поэтому в данной статье исследуется альтернативный подход к решению задачи цифровой фильтрации, основанный на прямом и обратном дискретном преобразовании Фурье. Как будет показано далее, такой подход позволяет не только заграждать частоты в области 0-0.6 Гц, как это делается в [4], а реализовать частотный фильтр с заданными полосами пропускания и заграждения во всем диапазоне частот от 0 до частоты Найквиста с практически “идеальной” АЧХ прямоугольной формы. Более того, при определенных модификациях обеспечивается возможность подавления отдельных фиксированных гармоник, что особенно важно при решении ряда практических задач, когда гармоническая помеха находится в области информативных частот полезного сигнала.
Алгоритм частотно-избирательной фильтрации. Рассматриваемый подход основан на использовании алгоритмов прямого FFT обратного IFFT дискретного преобразования Фурье (ДПФ), описанных в работах [8,9]. Известно [10], что эти алгоритмы взаимно обратимы (с точностью до малых погрешностей округления), т.е. для любого вектора Z справедливо равенство
IFFT(FFT (Z)) =Z. (3)
Отсюда, казалось бы следует, что если в векторе, полученном после прямого ДПФ провести обнуление элементов, соответствующих требуемым полосам режекции, то после обратного ДПФ будет получен отфильтрованный сигнал.
Вместе с тем оказывается, что такой достаточно простой прием эффективен лишь в том случае, когда частоты помехи кратны первой гармонике разложения Фурье. Дело в том, что только в этом частном случае спектр гармонической помехи, построенный на основании прямого ДПФ, будет адекватен реальному спектру помехи. Если же это условие не выполняется, то спектр гармонической помехи будет “распределяться” на целый ряд смежных гармоник.
Для иллюстрации этого эффекта рассмотрим спектры двух гармонических сигналов
z1[n] = sin (2πf1n) и z2[n] = sin (2πf2n) (4)
с частотами f1 = 16.5 Гц и f2 = 16.5165432768543 Гц. Заметим, что частоты сигналов практически совпадают.
На рис. 1. показаны фрагменты спектров этих сигналов, построенные на основании прямого ДПФ по N=30000 отсчетам при частоте дискретизации 1000 Гц. Как видно только в первом случае, когда частота сигнала совпала с одной из частот разложения Фурье, построенный спектр адекватен реальной ситуации (рис.1 а).

Рис.1. Спектры
гармонических сигналов z1
и z2:
а) f1 -
кратная частота; б) f2
-некратная частота
Однако на практике такой случай является скорее редким исключением, чем правилом. Отсюда следует, что если в общем случае для фильтрации гармонической помехи обнулять все гармоники, на которые распределилась нагрузка помехи, то это может затронуть гармоники, несущие информацию о полезном сигнале, и в результате после обратного преобразования Фурье полезный сигнал может быть существенно искажен.
Для устранения отмеченного недостатка нами предложен модифицированный алгоритм частотно-избирательной фильтрации, блок схема которого представлена на рис. 2.

Рис. 2. Блок схема алгоритма
В отличие от тривиального, алгоритм предусматривает процедуру модификации данных, поступающих на вход прямого ДПФ, обеспечивая эффект “контрастирования” спектра гармонической помехи. В результате после применения такой процедуры обнуление (либо снижение амплитуды) гармоник в области режекции и последующее обратное преобразование Фурье приводит к эффективному удалению помехи без заметных искажений полезного сигнала.
Результаты экспериментальных исследований. Для оценки эффективности разработанных алгоритмов проводились эксперименты на модельных и реальных сигналах. Такая оценка выполнялась согласно схеме, показанной на рис. 3.

Рис. 3. Схема эксперимента
Эксперимент 1: “Заграждение низких частот”. Модели эталонного сигнала и помехи представляли собой гармонические сигналы, сгенерированные в N =30000 точках при частоте дискретизации F =1000 Гц. Частота полезного сигнала составляла fx = 16.0123456789, частота помехи составляла fε =16.5123456789 Гц. Заметим, что в данном случае различие частот сигнала и помехи не превышает 0.1% частоты Найквиста.
На рис. 4. приведен фрагмент
спектра суммы данных гармоник до
(рис.4 а) и после (рис. 4 б) применения
процедуры контрастирования.

Рис.4. Спектр сигнала в эксперименте 1
а) до контрастирования, б) после контрастирования
Результат фильтрации представлен на рис. 5. Для сравнения на этом же рисунке представлен фрагмент эталонного сигнала. Сравнение фильтрованного и эталонного сигнала показало, что практически на всей области определения различия их значений не превышали 2 % диапазона изменения сигналов.

Рис.5. Результаты эксперимента 1
Эксперимент 2: “Заграждение высоких частот”. В условиях данного эксперимента частота полезного сигнала составляла fx = 250.123456789, а частота помехи - fε = 251.123456789 Гц. Сумма этих сигналов генерировалась в N =30000 точках при частоте дискретизации F =1000 Гц.
На рис. 6. приведен фрагмент
спектра суммы данных гармоник до
(рис.6 а) и после (рис. 6 б) применения
процедуры контрастирования.

Рис.6. Спектр сигнала в эксперименте 2
а) до контрастирования, б) после контрастирования
При фильтрации получен практически такой же результат (рис.7), как и в эксперименте 1.

Рис.7. Результаты эксперимента 2
Эксперимент 3. “Выделение полигармонического сигнала на фоне случайной помехи”. Полезный сигнал представлял собой сумму трех гармонических колебаний
x[n] = 12sin (2πf1n) +7sin (2πf2n +0.3) + 9sin (2πf3n +0.8)
с частотами f1 =15 Гц, f2 =50 Гц, f3= 75 Гц, различными амплитудами и фазами. Сигнал зашумлялся аддитивной случайной помехой, представляющей собой последовательность независимых величин, равномерно распределенных на интервале, равном 10% диапазона изменения сигнала x[n]. Сигнал генерировался в N =30000 точках при частоте дискретизации F =1000 Гц.
Как видно из рис. 8, на котором представлены результаты фильтрации, и в данном случае удалось достаточно эффективно восстановить эталонный сигнал.

Рис.8. Иллюстрация
результатов эксперимента 3:
зашумленный сигнал (а); фильтрованный
сигнал (б); эталонный сигнал (в)
Эксперимент 4. “Фильтрация электрокардиограммы”. В данном эксперименте в качестве эталонного сигнала была использована реальная ЭКГ, зашумленная гармонической помехой в области 16.7 Гц. Такая частота характерна для ряда условий эксплуатации кардиографических систем, но, в отличие от 50 Гц, непосредственно расположена в области информативных частот полезного сигнала.
При эксперименте амплитуда помехи составляла 100 % размаха эталонного сигнала. Сумма эталонной ЭКГ и помехи генерировалась в 30000 точек с частотой дискретизации F= 1000 Гц.
Сравнивались два способа фильтрации – без контрастирования спектра помехи и с контрастированием спектра помехи. Результаты тестирования (фрагменты сигналов) приведены на рис. 9
Как видно из рисунка, контрастирование спектра помехи в процессе фильтрации позволило избавиться от существенных искажений ЭКГ

Рис.9. Иллюстрация результатов эксперимента 4: эталонная ЭКГ (а); зашумленная ЭКГ (б); результат фильтрации без контрастирования спектра (в) и с контрастированием спектра (г)
Эксперимент 5. “Фильтрация магнитокардиограммы”. В данном эксперименте производилась фильтрация МКГ здорового пациента, которая была зарегистрирована в течение 30 сек при частоте дискретизации F=1000 Гц с использованием сверхчувствительного измерителя на основе сверхпроводящего квантового интерферометрического датчика. Измерение производилось в реальных клинических условиях без использования дорогостоящего экранированного помещения. Вследствие этого исходный сигнал был существенно искажен.
Фильтрация МКГ проводилась совокупностью цифровых фильтров, построенных на основе ДПФ, в том числе
Результат фильтрации оценивался визуально по внешнему виду фильтрованной МКГ (ввиду отсутствия эталона этого сигнала). При этом критерием оценки служило наличие на сигнале характерных фрагментов, отражающих работу предсердий и желудочков сердца в виде зубца P, комплекса QRS и сегмента ST-T. Результат фильтрации показан на рис. 10:
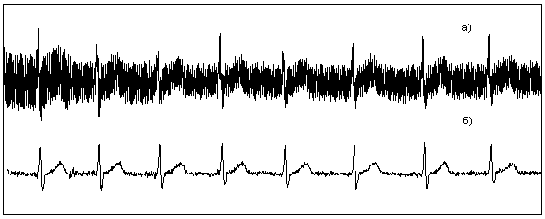
Дальнейшее улучшение качества обработки МКГ в реальной системе обеспечивалось применением специального алгоритма адаптивного сглаживания [11].
Заключение
Проведенные эксперименты подтвердили эффективность фильтрации гармонических помех на основе прямого и обратного ДПФ на реальных и модельных данных. Метод позволяет реализовать узкополосный заградительный фильтр в диапазоне от частот 0 до частоты Найквиста. При этом полоса режекции может составлять величину меньшую 0.1% частоты Найквиста, что существенно при обработке биомедицинских сигналов (например ЭКГ и МКГ), когда гармоническая помеха располагается в области информативных частот полезного сигнала.
Эксперименты проводились с использованием компьютера Pentium II c тактовой частотой 850 МГц и оперативной памятью 256 Мб. При этом время фильтрации реальных ЭКГ и МКГ, зарегистрированных в течение времени 30 сек с частотой дискретизации 1000 Гц, не превышало 0.03 сек, что вполне допустимо для практического применения.
Автор выражает благодарность Н.В. Прогонному за участие в программной реализации алгоритма и обсуждение результатов тестирования.
ЛИТЕРАТУРА:
|
| О проекте | Контакты | Архив старого сайта |
|
Copyright © SciTecLibrary © 2000-2017 | ||